Continuing on from the previous blog on the same subject, https://www.si-eng.org/blog/a-step-by-step-anatomy-of-concrete-stress-strain-curve-1
this one goes on further to touch on the stiffness of concrete and the simplified relationships for cross-sectional design.
Stiffness
The previous blog has explained that since early stage, the stress-strain behaviour of concrete has begun to be non-linear. The stiffness of concrete is significantly larger under small stress. The larger the stress is, the smaller the stiffness of concrete gets. Once the stress gets close to the ultimate stress capacity of concrete, the incremental stiffness for each stress increase drops substantially.
This non-linearity is a problem for calculating material stiffness, as the fundamental assumption for elastic modulus is that the behaviour is linear. It is impossible to use a single constant modulus to represent a non-linear curve. Nevertheless, two commonly used ways of expressing elastic modulus of concrete is used – the tangent modulus of elasticity Ec, and the secant modulus of elasticity Ecm.
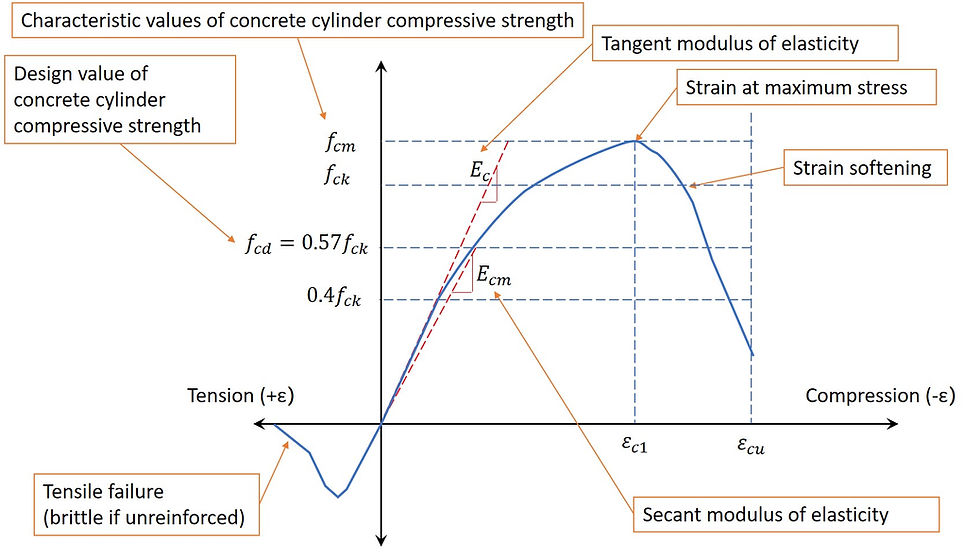
In Eurocode, Ecm is normally used. Ec is rarely used, and even when used, is calculated based on Ecm. Why? This is because design using Ecm gives you more deformation which is typically more conservative. It is ultimately the strain that breaks concrete not the stress. As you can see from the diagram, the tangent modulus is higher than the secant modulus. When the compressive stress in the concrete is controlled within the code design limit fcd, we can see the difference between the two is very marginal. EC2 allows you to use Ec=1.05Ecm.
At low stress levels, using Ecm is over estimating the strain, which is fine. But at high stress levels, using Ecm is under estimating the strain, which is dangerous. Fortunately this has been taken care of by limiting the stress levels in the concrete to design values fcd.
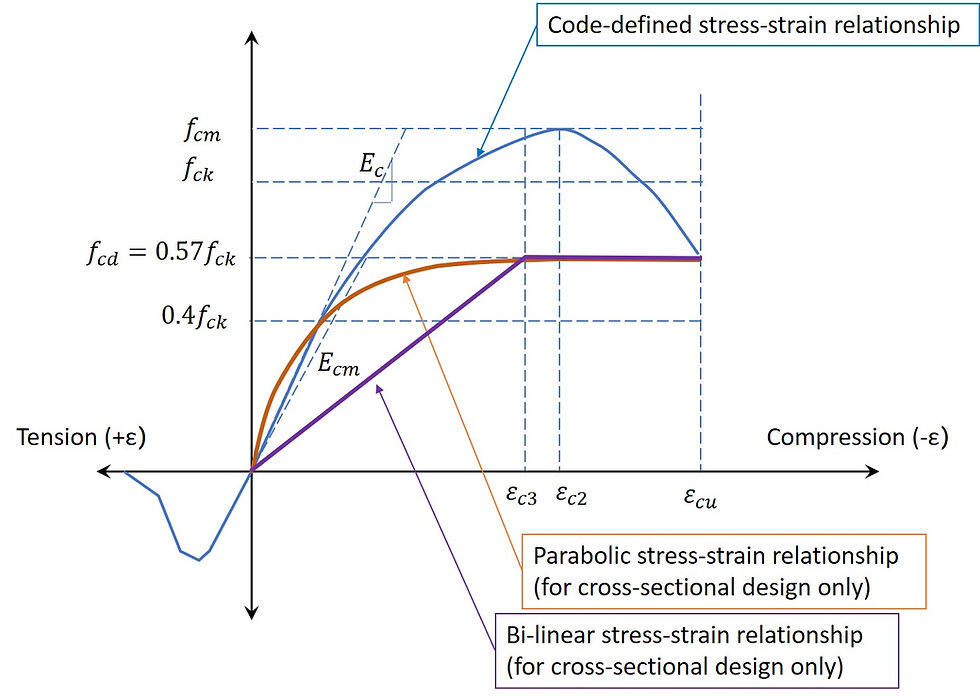
Bi-linear and parabolic stress-strain relationship
The previous blog explained that two versions of simplified stress-strain curves are allowed in Eurocode – b-linear and parabolic. The difference between the two can be suttle or significant depending on the stress conditions of the concrete – whether the stress is high or low.
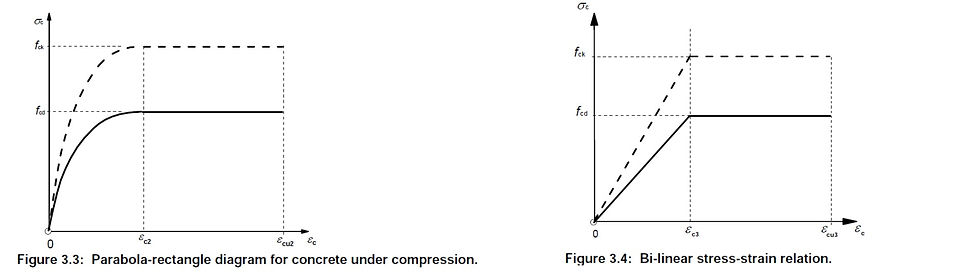
Two advantages of parabolic relationship are:
1) The yield stress εc2 is more than that of the bi-linear relationship εc3, hence able to utilise the capacity more fully. 1750 bi-linear microstrain vs. 2000 microstrain for parabola. In other words, the concrete yields earlier in bi-linear relationship than the parabolic one.
2) The design stiffness of concrete is higher for parabolic curve. In other words, for the same given loading, concrete designed to parabolic curve will have less deformation.
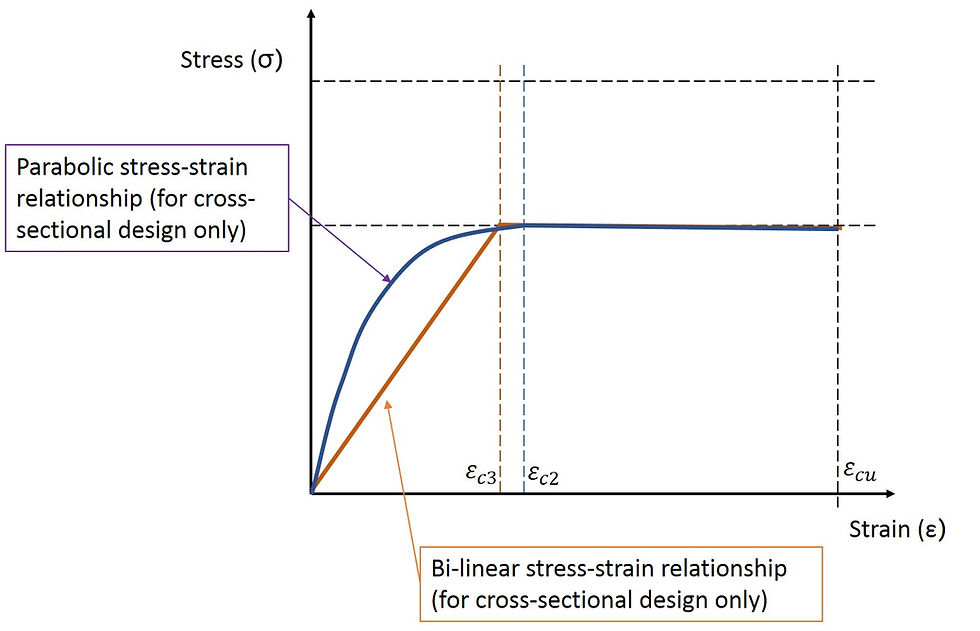
The only weakness of the parabolic relationship is that it is more tricky to use and can only be achieved by computerised calculations.
Nevertheless we should bear in mind that these two models should only be used when designing cross-sections, as they are simplified and deviate from the real behaviour.
Comments